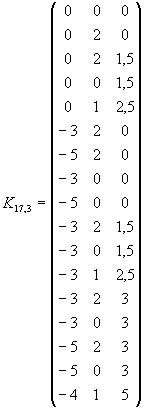
Im R³ werden Punkte nun nicht mehr mit zwei Koordinaten, sondern mit drei Koordinaten (x, y, z) dargestellt. Demnach müssen nicht nur die bisher erarbeiteten Abbildungsmatrizen abgeändert werden, sondern insbesondere muss auch die Kirchenmatrix K10,2 erweitert und an den R³ angepasst werden.
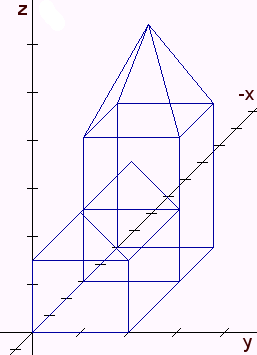
Im R³ lässt sich die Kirche nicht mehr durch 10 Punkte darstellen, sehr wohl aber durch 17 Punkte, welche ebenfalls wieder verschieden miteinander verbunden werden. Die Punkte haben jeweils drei Koordinaten. Die Matrix K10,2 muss also in die Matrix K17,3 abgeändert werden, wobei die Elemente ki,1, ki,2 und ki,3 die drei Koordinaten xi, yi und zi des Punktes Pi darstellen.
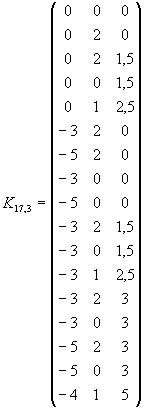

Zunächst einmal kann wieder davon ausgegangen werden, dass ein Punkt P(x, y, z) auf einen Punkt P'(x', y', z') abgebildet werden soll. Hierzu lässt sich wieder folgendes Gleichungssystem aufstellen:
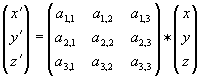
Kombiniert man nun diese Matrizengleichung mit der für den R² berechneten Drehmatrix, so erhält man folgende Drehmatrizen für den R³:
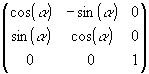
![]() Drehung um die z-Achse
Drehung um die z-Achse
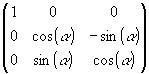
![]() Drehung um die x-Achse
Drehung um die x-Achse
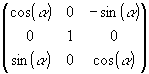
![]() Drehung um die y-Achse
Drehung um die y-Achse
Beachtet man nun noch unter der Einführung homogener Koordinaten für den R³ eine möglich Verschiebung um den Vektor (vx vy vz), so erhält man die allgemeine Matrix A4,4, welche im R³ eine affine Abbildung mittels homogener Koordinaten durchführt:
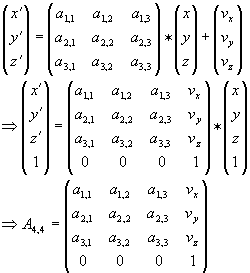
Es kann manchmal passieren, dass für eine gewünschte Abbildung mehrere Einzelabbildungen hintereinander notwendig sind. Wird dann die gewünschte Abbildung auch noch öfter verwendet, so kann es sinnvoll sein, die Einzelabbildungen zu einer einzigen Abbildungsmatrix zusammen zu fassen.
Veranschaulichen kann ich dieses Problem wieder an der Kirche:
Soll diese zum Beispiel öfter um den Punkt G(4, 2, -1) in der xy-Ebene gedreht werden, so wäre es praktisch, wenn eine Drehmatrix A mit diesen Eigenschaften zur Verfügung stände.
Auf einfachem Wege müßte man die Kirche K sowie den Punkt G erst so verschieben, dass G auf dem Ursprung (0, 0, 0) zu liegen käme. Dann könnte man um die z-Achse drehen, und danach die Kirche sowie den Punkt G wieder zurückschieben, um den entgegengesetzten Vektor wie bei der ersten Verschiebung.
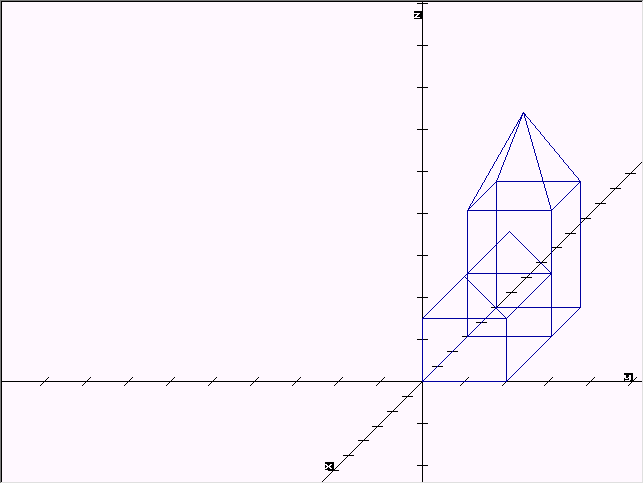
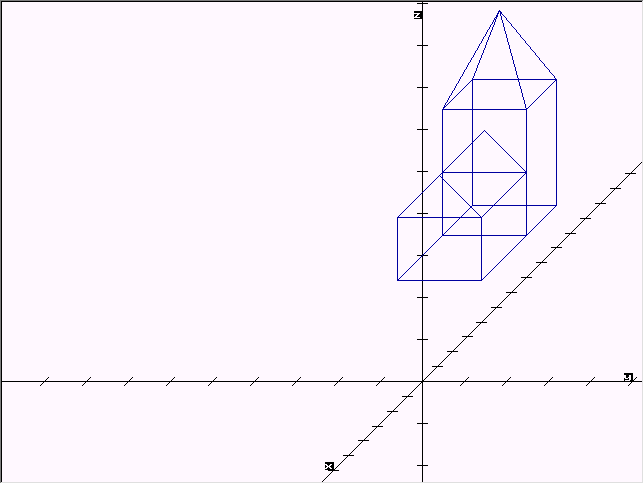
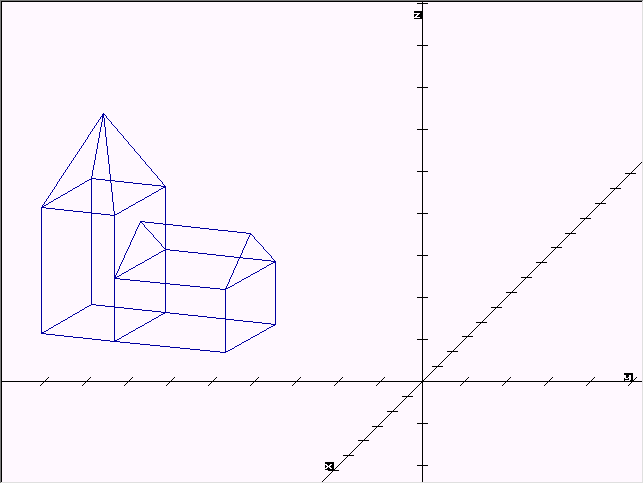
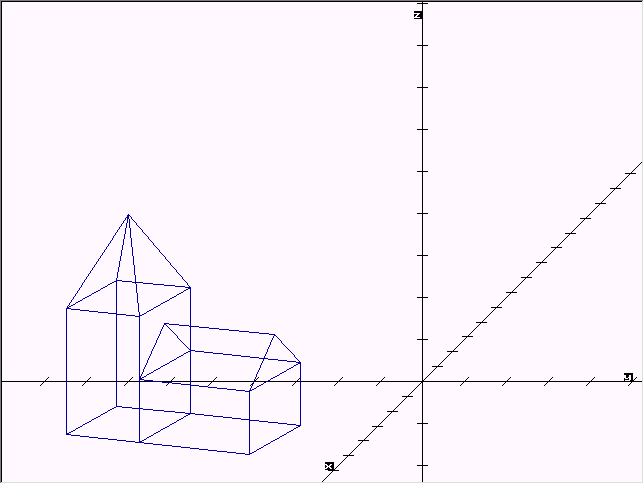
Die drei Matrizen B (erste Verschiebung), C (Drehung) und D (zweite Verschiebung) sollen jetzt zu einer Matrix A zusammen gefasst werden.
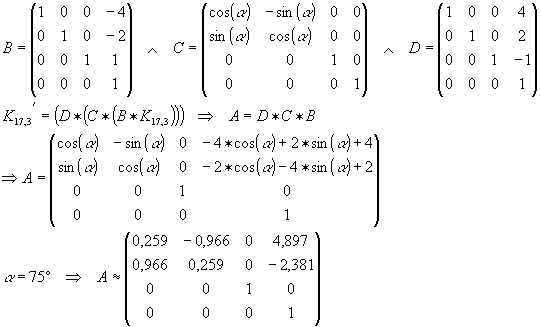
Die Matrix A würde also ein Objekt um den Punkt G in der xy-Ebene mit dem Winkel α (75°) drehen.